Logistic Regression: Sex
- Will run the code together
- ~60 Minutes
- Followed By: Goodbye!

PASSENGERS
If you deleted/lost the passengers data set, run this:
source("http://choens.github.io/titanic/workshops/regression/import-passengers.R")
Be careful using a command like source()

Learning Objectives
- Define Logistic Regression
-
Survived becomes died!
We will create a new column (Died) - Logistic Regression
- Visualizing Logistic Regression
- Calculating Odds Ratio
Logistic Regression
- A regression model with a categorical dependent variable. Today's workshop covers the case of a binary dependent variable, which has only two values, "0" and "1", which represent outcomes such as alive/dead.
- Developed by statistician David Cox in 1958. Used to estimate the probability of a binary response based on one or more predictor variables. It allows one to say the presence of a risk factor affects the probability of a given outcome by a specific percentage.
- For more information, see Wikipedia
Survived
- Survived could be a good dependent variable (outcome).
tbl_surv <- table(passengers$survived)
tbl_surv
0 1
140 110
100*prop.table(tbl_surv)
0 1
56 44
## The sample low-balls the death-rate.
Died!
- Need a new column; Epis are always positive.
- Usually discuss risk factors.xb
- Easier to type
diedthansurvived.
passengers$died <- 1
passengers$died[passengers$survived == 1] <- 0
## These two cols should be opposites.
## Or, you did something silly.
passengers[,c("survived", "died")]
survived died
1 0 1
2 1 0
3 1 0
4 1 0
5 0 1
6 0 1
7 1 0
8 1 0
9 0 1
10 0 1
11 1 0
12 0 1
13 0 1
14 1 0
15 0 1
16 0 1
17 0 1
18 0 1
19 1 0
20 0 1
21 1 0
22 1 0
23 0 1
24 0 1
25 1 0
26 0 1
27 0 1
28 0 1
29 1 0
30 0 1
31 0 1
32 1 0
33 0 1
34 0 1
35 0 1
36 1 0
37 0 1
38 0 1
39 0 1
40 0 1
41 0 1
42 0 1
43 1 0
44 1 0
45 1 0
46 0 1
47 0 1
48 0 1
49 0 1
50 0 1
51 0 1
52 0 1
53 0 1
54 0 1
55 1 0
56 0 1
57 0 1
58 0 1
59 0 1
60 0 1
61 1 0
62 1 0
63 1 0
64 1 0
65 1 0
66 1 0
67 0 1
68 0 1
69 0 1
70 1 0
71 0 1
72 0 1
73 1 0
74 1 0
75 0 1
76 0 1
77 0 1
78 1 0
79 0 1
80 0 1
81 1 0
82 1 0
83 0 1
84 0 1
85 0 1
86 1 0
87 1 0
88 1 0
89 1 0
90 0 1
91 0 1
92 1 0
93 1 0
94 0 1
95 0 1
96 1 0
97 0 1
98 1 0
99 1 0
100 0 1
101 1 0
102 1 0
103 1 0
104 1 0
105 0 1
106 0 1
107 0 1
108 0 1
109 1 0
110 0 1
111 0 1
112 1 0
113 0 1
114 0 1
115 1 0
116 0 1
117 0 1
118 1 0
119 0 1
120 1 0
121 1 0
122 0 1
123 0 1
124 0 1
125 0 1
126 1 0
127 1 0
128 1 0
129 0 1
130 1 0
131 0 1
132 1 0
133 0 1
134 1 0
135 0 1
136 1 0
137 1 0
138 1 0
139 0 1
140 0 1
141 1 0
142 1 0
143 0 1
144 0 1
145 0 1
146 1 0
147 1 0
148 1 0
149 0 1
150 0 1
151 1 0
152 0 1
153 0 1
154 1 0
155 1 0
156 0 1
157 1 0
158 1 0
159 1 0
160 0 1
161 0 1
162 1 0
163 1 0
164 0 1
165 1 0
166 1 0
167 0 1
168 1 0
169 1 0
170 1 0
171 0 1
172 0 1
173 1 0
174 1 0
175 0 1
176 1 0
177 1 0
178 1 0
179 1 0
180 0 1
181 0 1
182 0 1
183 0 1
184 1 0
185 0 1
186 0 1
187 1 0
188 1 0
189 1 0
190 0 1
191 0 1
192 0 1
193 1 0
194 0 1
195 0 1
196 0 1
197 1 0
198 1 0
199 0 1
200 1 0
201 1 0
202 1 0
203 0 1
204 0 1
205 1 0
206 1 0
207 0 1
208 1 0
209 0 1
210 0 1
211 1 0
212 0 1
213 0 1
214 1 0
215 0 1
216 1 0
217 1 0
218 0 1
219 0 1
220 0 1
221 0 1
222 0 1
223 1 0
224 0 1
225 1 0
226 1 0
227 0 1
228 1 0
229 0 1
230 1 0
231 0 1
232 1 0
233 1 0
234 0 1
235 0 1
236 1 0
237 1 0
238 0 1
239 0 1
240 0 1
241 1 0
242 0 1
243 0 1
244 0 1
245 0 1
246 0 1
247 1 0
248 0 1
249 0 1
250 0 1
Logistic Regression: Categorical
- Independent variable:
sex - Dependent variable:
died
## Cannot have NAs in our data.
sum(is.na(passengers$sex))
[1] 0
sum(is.na(passengers$died))
[1] 0
## We cannot graph this regression with a categorical.
## We can graph a numeric variable.
## This will make sense in a slide or two.
passengers$is_male <- 0
passengers$is_male[passengers$sex == "male"] <- 1
## To what extent does is_male explain our outcome, died?
logit_sex <- glm(formula=died~is_male, family=binomial, data=passengers)
Output on next slide.
Died~Sex
- Formula: died as a function of sex
- Sex is a statistically significant predictor of died.
- Reduces residual deviance and AIC.
summary(logit_sex)
Call:
glm(formula = died ~ is_male, family = binomial, data = passengers)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.7125 -0.8112 0.7244 0.7244 1.5948
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.9426 0.2152 -4.380 1.19e-05 ***
sexmale 2.1466 0.2928 7.332 2.27e-13 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 342.96 on 249 degrees of freedom
Residual deviance: 281.47 on 248 degrees of freedom
AIC: 285.47
Number of Fisher Scoring iterations: 4
Visualizing: Died~Sex
plot(jitter(passengers$died, .4),
jitter(passengers$is_male, .4))
curve(predict(logit_sex, data.frame(is_male=x), type="response"), add=TRUE)

Logistic Regression: Continuous
- Independent variable:
age - Dependent variable:
died
## Cannot have NAs in our data.
sum(is.na(passengers$age))
[1] 0
sum(is.na(passengers$died))
[1] 0
## To what extent does the variable age explain our outcome, died?
logit_age <- glm(formula=died~age, family=binomial, data=passengers)
Output on next slide
Died ~ Age
- Formula: died as a function of age
- Age is not a statistically significant predictor of died!
AlmostNo difference to residual deviance or AIC.- Why is this a bad model?
summary(logit_age)
Call:
glm(formula = died~age, family = binomial, data = passengers)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.366 -1.273 1.037 1.089 1.145
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.063888 0.303464 0.211 0.833
age 0.005861 0.009127 0.642 0.521
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 342.96 on 249 degrees of freedom
Residual deviance: 342.55 on 248 degrees of freedom
AIC: 346.55
Number of Fisher Scoring iterations: 4
Visualizing: Died~Age
plot(passengers$age, passengers$died)
curve(predict(g_age, data.frame(age=x), type="response"), add=TRUE)
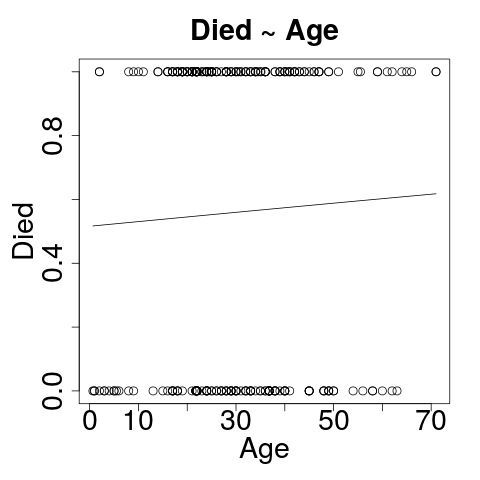
Yeah - That's supposed to be curved.
Let's Cheat for a moment
- GAM: Generalized Additive Model
- Not doing these today, but you need to understand.
- Several confounders here. What can we do?
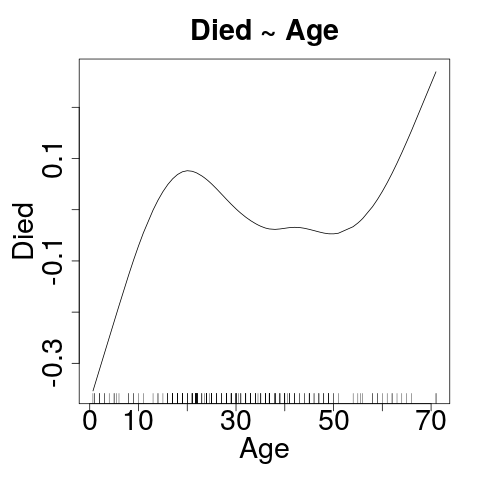
Click on the image to make it easy to really LOOK at it.
Suggestions?
- How can we use age to predict died?

New Factors
- First we explore. And we need new tricks.
## You've seen this:
prop.table(table(passengers$died))
0 1
0.44 0.56
## Indexing / Filtering: What percent of passengers
## five years or age or younger died?
prop.table(table(passengers$died[passengers$age <= 5]))
0 1
0.8181818 0.1818182
## Note: I'm TIRED of typing passengers.
New Tricks
with |
&, | |
round |
## - Only write passengers once
## - Percentage of passengers died who are older than 5
## and younger than 11.
with(passengers,
prop.table(table(died[age > 5 & age <= 10]))
)
0 1
0.5714286 0.4285714
## Make the percentage easier to grok:
with(passengers,
round(prop.table(table(died[age > 5 & age <= 10]))*100)
)
Age Group, Not Age
## Let's create a new factor:
passengers$age_group <- NA
passengers$age_group[passengers$age <= 10] <- "00-10"
passengers$age_group[passengers$age > 10 & passengers$age <= 20] <- "11-20"
passengers$age_group[passengers$age > 20 & passengers$age <= 30] <- "21-30"
passengers$age_group[passengers$age > 30 & passengers$age <= 40] <- "31-40"
passengers$age_group[passengers$age > 40 & passengers$age <= 50] <- "41-50"
passengers$age_group[passengers$age > 50 & passengers$age <= 60] <- "51-60"
passengers$age_group[passengers$age > 60] <- "61+"
Complex Tables
## This should be familiar by now:
with(passengers,
round(prop.table(table(age_group, died),1)*100,1))
## But this is nice!
multi_tbl <- with(passengers,
round(prop.table(table(age_group, sex, died),1)*100,1))
ftable(multi_tbl)
age_group sex
00-10 female 27.8 22.2
male 44.4 5.6
11-20 female 24.3 13.5
male 5.4 56.8
21-30 female 31.3 14.5
male 10.8 43.4
31-40 female 41.7 10.0
male 10.0 38.3
41-50 female 21.2 9.1
male 18.2 51.5
51-60 female 40.0 0.0
male 10.0 50.0
61+ female 11.1 0.0
male 11.1 77.8
 Your Turn!
Your Turn!
-
Is
age_groupa statistically significant predictor ofdied? - No peeking!
Died~Age_Group Is Better
logit_age <- glm(formula=died~age_group, family=binomial, data=passengers)
summary(logit_age)
Call:
glm(formula = died ~ age_group, family = binomial, data = passengers)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.734 -1.177 0.840 1.047 1.601
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.9555 0.5262 -1.816 0.06941 .
age_group11-20 1.8157 0.6374 2.849 0.00439 **
age_group21-30 1.2714 0.5713 2.226 0.02604 *
age_group31-40 0.8888 0.5862 1.516 0.12948
age_group41-50 1.3863 0.6355 2.181 0.02915 *
age_group51-60 0.9555 0.8228 1.161 0.24550
age_group61+ 2.2083 0.9591 2.303 0.02130 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 342.96 on 249 degrees of freedom
Residual deviance: 330.08 on 243 degrees of freedom
AIC: 344.08
Number of Fisher Scoring iterations: 4
Tweak these groups to reduce the residuals further.
But don't overfit.
 Your Turn!
Your Turn!
- There are two logistic regression models below.
- One model is definitely better than the other. Why?
logit_complex <- glm(formula = died ~ age_group+is_male, family = binomial, data = passengers)
summary(logit_complex)
logit_complex <- glm(formula = died ~ age_group*is_male, family = binomial, data = passengers)
summary(logit_complex)
?formula
Odds Ratio
- This is for the epidemiologists.
- No Base R function to calculate odds ratio.
- But, it isn't hard to calculate it.

Odds Ratio (OR)
- Quantifies how strongly the presence or absence of property A is associated with the presence or absence of property B in a given population.
- We want to know how being male is associated with dying.
- Focus is on the Odds Ratio and not Risk Ratio because of the relationship between OR and logistic regression.
OR: First Steps
- Need the odds of dying for two different groups.
- We need a 2x2 table: died x is_male
- This table is backwards from how this is usually shown in text books.
- Could invert the table, or just do the math right.
## Remember: Rows (died), Columns (is_male)
t_male <- with(passengers,
table(died, is_male, dnn=c("died","is_male"))
)
t_male
is_male
died 0 1
0 77 33
1 30 110
## Yeah. Those numbers alone tell you alot.
The odds of dying:
| Man: |
110/33
|
| Woman: |
30/77
|
The ratio of these two odds:
(110/33)/(30/77)
|
or . . . |
(110*77)/(33*30)
|
- The Odds Ratio in our sample is 8.555555555555555 . . .6
- That is an enormous risk factor.
 Your Turn!
Your Turn!
Can you figure out how to do that with R?
It is just some fancy indexing trickery.
OR: Algebraic Method
## Remember:
t_male
is_male
died 0 1
0 77 33
1 30 110
Thus, our solution . . .
## Remember, you can use R like a giant calculator:
(t_male[2,2] * t_male[1,1]) / (t_male[2,1]*t_male[1,2])
[1] 8.555556
## This does not come with confidence intervals.
Pop Quiz!
What is the relationship between OR and logistic regression?
-
The
log()of the OR == the coefficient from the logit model. - Which means . . .
-
The
exp()of the coefficient from the logic model == the OR. - If you can build the logit model, the OR is one step away.
Deriving OR from logit model
## How does this help us?
names(summary(logit_sex))
Deriving OR from logit model
- This is one way to do it.
## Step 1: Access the model coefficients:
summary(logit_sex)$coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.942608 0.2152215 -4.379712 1.188363e-05
is_male 2.146581 0.2927698 7.331975 2.267860e-13
## Step 2: Calculate the exponent of the coefficients:
exp( summary(logit_sex)$coefficients )
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.3896104 1.240137 1.252897e-02 1.000012
is_male 8.5555556 1.340134 1.528397e+03 1.000000
Deriving OR from logit model
- This is another way to do it.
## Step 1: Access the model coefficients:
logit_sex_coef <- summary(logit_sex)$coefficients
## Step 2: Calculate the exponent of the coefficients:
exp( logit_sex_coef )
## - Step 1 returns a vector and saves it as logit_sex_coef.
## - Step 2 calculates the exponent for each item in the vector.
##
## Using R is like building a spaceship with LEGOS!
## Assemble little things to build big things.
Next Week's R Workshop
The following ad is paid for by our sponsors.
- What holds you back from using R?
- Next week, complete a project!
-
This includes:
- Download data from OpenData NY
- Explore the data
- Build a reproducible report (HTML/Word)
- Discuss advanced topics like reproducible research, automation, etc.

 Your Turn!
Your Turn!
- Can you create a better regression model?
- Please complete the workshop survey
- I am trying to plan our afternoon on the 22nd.
I would like to know what kinds of analyses YOU would like to be able to do in R. Please email me at andy.choens@acuitashealth.com, with your ideas.
Some/all (depends) will make it into the afternoon of the 22nd.